Shor Algorithm by the Numbers

Research Links

• CSE 599d – Quantum Computing Shor’s Algorithm
• CSE 599d
• Quantum Algorithms
• Chapter 10 of the book: Algorithms
• Book: Algorithms

Simulating the quantum factoring process in Open Office Calc

• Shor Algorithm in Open Office Calc
• How to calculate greatest common factor in open office calc
• Open Office Calc: Conditional formating
• DFT on OpenOffice Calc
• Gnumeric – a spreadsheet that has high accuracy and built in FFT
• An Overview of an OpenOffice.org Basic Program
• Tutorial covering using basic in open office
• Fourier analysis tool in Microsoft Excel
• List of prime numbers

Umesh V. Vazirani

• Umesh V. Vazirani  webpage with publication links
• CS191 – Class notes

---

Numeric Example of the Shor Algorithm

Beforehand we keep in mind the solution and watch the method unfold.  See Chapter 10 of the book: Algorithms  for greater detail.

LibreOffice SpreadSheet with these same calculations:  Shor-Algorithm-By-The-Numbers-Amarketplaceofideas-com.ods

Pick:   

 

 

 

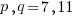
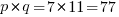
Factor 77 using Shor's algorithm

Pick relative prime = 5. 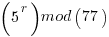   will be periodic in r.   The following would be set up in a quantum register to have all the values in the register simultaneously and calculate the function results simultaneously.

  

 

 

 

 

 

  

 

 

 

 

 

 

 

 

  

 

 

 

 

 

 

 

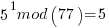
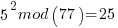
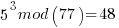
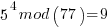
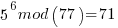
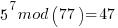
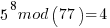
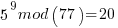
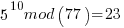
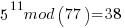
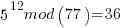
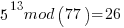
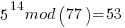
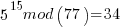
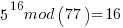
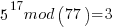
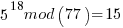
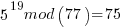
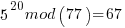
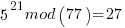
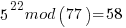
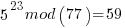
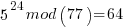
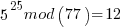
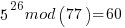
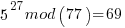
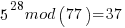
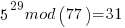
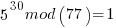  ……… here we see the form of even power of the variable with 1 left over after the mod.  That gives the  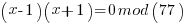 form

 

 

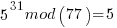
After the above results are piled simultaneously in the quantum register a quantum FFT is performed and the period r found to be 30 with high probability.     All the above mod result values are in the register at the same time and not indexed per time or pure number index as far as I know.  A quantum FFT does not yield a spectrum.  It yields a frequency estimate of highest probability of the input waveform.   Frequency as in probability frequency.  However the above mod result values are KNOWN to be in regular spacing so a frequency that we are accustomed to can be calculated.

Thus using

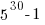       have common factors with 77.  

     

 

Each of 77's 2 coprime factors have a common factor with only  one of the 2 terms above.   Use Euclid's rule to find the greatest common denominator.  See chapter 1.2.3 of Algorithms.

Demonstrate this to yourself by using greatest common factor calculator webpage with ( 77,30517578126)  & ( 77,30517578124)

   

   

 

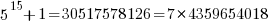
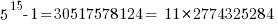
This yields    

     77= 7 * 11      

and the problem is solved.  

---

More Links

• Shor I'll do it
• Overview of Shor's algo
• Experimental demonstration of Shor's algo