Intuitive Matrix Inverse

$A = matrix{3}{3}{a_11 a_12 a_13 a_21 a_22 a_23 a_31 a_32 a_33}^-1 = matrix{3}{3}{a^c_11 a^c_12 a^c_13 a^c_21 a^c_22 a^c_23 a^c_31 a^c_32 a^c_33}^T /Delta$

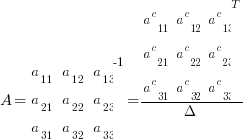
Where superscript c denotes the cofactor of the matrix element and Delta is the determinant of A

If you evaluate the row=1 , column=1 product of the original matrix with its inverse you see row=1 X column=1 results in:

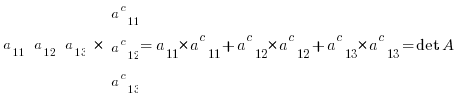$matrix{1}{3}{a_11 a_12 a_13 a_21 a_22 a_23 a_31 a_32 a_33} * matrix{3}{1}{a^c_11 a^c_12 a^c_13} = a_11 * a^c_11 + a^c_12 * a^c_12 + a^c_13 * a^c_13 = det A$ ……( duh! what a setup. elements times cofactors sum to determinant by definition! )

Which is what you would expect without having introduced the scaling factor of determinant of A. In fact what happens is any main diagonal position results in the same value.

If you evaluate the row=2 column=1 product it is equivalent determinant of the following matrix:

$A = matrix{3}{3}{a_21 a_22 a_23 a_21 a_22 a_23 a_31 a_32 a_33}$

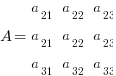
and since it has duplicate rows the determinant will always equal zero. It is easy to see all off diagonal values will result in the same condition. Thus by this method you can rapidly see the internal workings of how and why a matrix inverse works. No more mysteries with an infinity of steps deriving the matrix inverse. Now you can can just see it all at once in your head!

0 Comments

Leave a Reply