Solution of similtaneous linear equations

$A = (matrix{3}{3}{a_11 a_12 a_13 a_21 a_22 a_23 a_31 a_32 a_33}) (matrix{3}{1}{X_1 X_2 X_3 }) = (matrix{3}{1}{b_1 b_2 b_3 })$

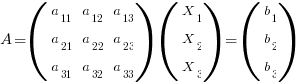
Multiplying the first column by 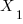X_1 alters the determinant as follows:

$det (matrix{3}{3}{a_11*X_1 a_12 a_13 a_21*X_1 a_22 a_23 a_31*X_1 a_32 a_33}) = X_1 * det(A)$

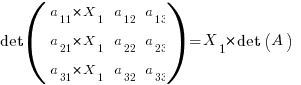
Now you can multiply the other columns and add to the first column to your hearts content as it does not alter the determinant due to linear dependency on the other rows.

Multiply column 2 by 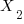and add to column 1
Multiply column 3 by 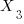and add to column 1

$det (matrix{3}{3}{ a_11*X_1+a_12*X_2+a_13*X_3 a_12 a_13 a_21*X_1+a_22*X_2+a_23*X_3 a_22 a_23 a_31*X_1+a_32*X_2+a_33*X_3 a_32 a_33}) = X_1 * det(A)$

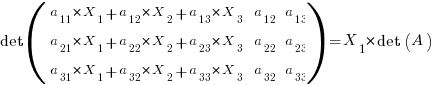
Woot! That first column now looks like the b vector! Substitute:

$det (matrix{3}{3}{ b_1 a_12 a_13 b_2 a_22 a_23 b_3 a_32 a_33}) = X_1 * det(A)$

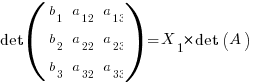
Dividing both sides by 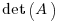det(A) yields

${det (matrix{3}{3}{ b_1 a_12 a_13 b_2 a_22 a_23 b_3 a_32 a_33})}/ {det(A)} = X_1$

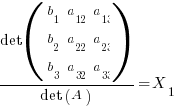
Which lends itself to the following form:

$(matrix{1}{3}{b_1 b_2 b_3}) * (matrix{1}{3}{{A_11}^c {A_21}^c {A_31}^cgt}) = X_1*det(A)$

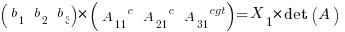
Where c denotes the cofactor of the associated matrix element

Observations

The solution does not depend on the direction of the 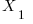coefficients
The solution is scaled by the 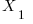coefficients
There is alot that can be said to be "vector like". The scaled and added columns are in the same direction as the other columns. ( basis vectors ?) And thus the cross product yields zero!
Dot product of b vector with cross product generated cofactor vector shows the solution to be in the direction of the cofactor vector scaled by the projection of b and det(A)
Cofactor vector is orthogonal to all the other column vectors showing that only the component of b in the orthogonal direction is what counts in the solution

References

Solution of similtaneous linear equations

0 Comments

Leave a Reply