Euclidean Algorithm for Greatest Common Denominator
Research Links

A 24-by-60 rectangle is covered with ten 12-by-12 square tiles, where 12 is the GCD of 24 and 60. More generally, an a-by-b rectangle can be covered with square tiles of side-length c only if c is a common divisor of a and b. So the task is to find the largest square that tiles the rectangle completely. See below:

Subtraction-based animation of the Euclidean algorithm. The initial rectangle has dimensions a = 1071 and b = 462. Squares of size 462×462 are placed within it leaving a 462×147 rectangle. This rectangle is tiled with 147×147 squares until a 21×147 rectangle is left, which in turn is tiled with 21×21 squares, leaving no uncovered area. The smallest square size, 21, is the GCD of 1071 and 462.
So the example compiled down to arithmetic steps would be as follows:
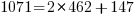
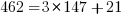
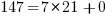 Thus 21 is the GCD of 1071 & 462
Thus 21 is the GCD of 1071 & 462
0 Comments