MOSFET Depletion Region Electric Field and Charge Density Forms
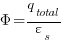
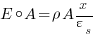
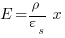
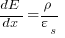
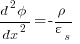 which is Poisson's equation.
which is Poisson's equation.
Substitute the depletion region charge density

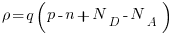 at the surface
at the surface
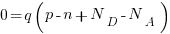 far from the surface
far from the surface
Subtracting:
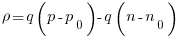
| Depletion Derivation Line | Inversion Derivation Line |
![{rho}= q(p-p_0)=q{p_0}[e^{{-phi}/{phi_t}}-1] {rho}= q(p-p_0)=q{p_0}[e^{{-phi}/{phi_t}}-1]](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_982_87c08a76fb9584c921598b6eb2de34c1.png)
|
![{rho}= -q(n-n_0)=-q{n_0}[e^{{phi}/{phi_t}}-1]=-q{{{n_i}^2}/{p_0}^2}{p_0}[e^{{phi}/{phi_t}}-1] {rho}= -q(n-n_0)=-q{n_0}[e^{{phi}/{phi_t}}-1]=-q{{{n_i}^2}/{p_0}^2}{p_0}[e^{{phi}/{phi_t}}-1]](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_975_f51ac280811302ccaecb7658a29fcb56.png) 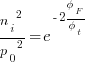
|
![{{d^2{phi}}/dx^2} = {{-qp_0}/{varepsilon_s}} {[e^{{-phi}/{phi_t}}-1]} {{d^2{phi}}/dx^2} = {{-qp_0}/{varepsilon_s}} {[e^{{-phi}/{phi_t}}-1]}](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_ff50f6d21d38c108d307333d2bfcf2ef.png)
|
![{{d^2{phi}}/dx^2} = {{qp_0}/{varepsilon_s}}{e^{{-2{phi_F}}/{phi_t}}}{[e^{{phi}/{phi_t}}-1]} {{d^2{phi}}/dx^2} = {{qp_0}/{varepsilon_s}}{e^{{-2{phi_F}}/{phi_t}}}{[e^{{phi}/{phi_t}}-1]}](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_6e7992f8c06c2dc59a1380d24fd30808.png)
|
![int{0}{phi_s}{2{{d^2{phi}}/dx^2}{d{phi}/{dx}}} = {{-2qp_0}/{varepsilon_s}} int{0}{phi_s}{{[e^{{-phi}/{phi_t}}-1]} {{d{phi}}/{dx}}} int{0}{phi_s}{2{{d^2{phi}}/dx^2}{d{phi}/{dx}}} = {{-2qp_0}/{varepsilon_s}} int{0}{phi_s}{{[e^{{-phi}/{phi_t}}-1]} {{d{phi}}/{dx}}}](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_957_3f45fa3c23412fd8fe024c7f1ac4af7e.png)
|
![int{0}{phi_s}{2{{d^2{phi}}/dx^2}{d{phi}/{dx}}} = {{-2qp_0}/{varepsilon_s}}{e^{-2{phi_F}/{phi_t}}} int{0}{phi_s}{{[e^{{phi}/{phi_t}}-1]} {{d{phi}}/{dx}}} int{0}{phi_s}{2{{d^2{phi}}/dx^2}{d{phi}/{dx}}} = {{-2qp_0}/{varepsilon_s}}{e^{-2{phi_F}/{phi_t}}} int{0}{phi_s}{{[e^{{phi}/{phi_t}}-1]} {{d{phi}}/{dx}}}](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_957_1252d113ad5c054a8105bff17e324a12.png)
|
![({d{phi}}/{dx})^2 = {{2qp_0}/{varepsilon_s}} {[{phi_t}e^{{-phi}/{phi_t}}+{phi}]} ({d{phi}}/{dx})^2 = {{2qp_0}/{varepsilon_s}} {[{phi_t}e^{{-phi}/{phi_t}}+{phi}]}](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_566849eacf34a4cf8e2311b9b11091a3.png)
|
![({d{phi}}/{dx})^2 = {{2qp_0}/{varepsilon_s}}{e^{-2{phi_F}/{phi_t}}} {[{phi_t}e^{{phi}/{phi_t}}+{phi}]} ({d{phi}}/{dx})^2 = {{2qp_0}/{varepsilon_s}}{e^{-2{phi_F}/{phi_t}}} {[{phi_t}e^{{phi}/{phi_t}}+{phi}]}](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_987c4e7a30773cda3cfbc004d8261f2a.png) right hand side evaluated 0 to right hand side evaluated 0 to 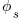
|
![({d{phi}}/{dx})^2 = {{2qp_0{phi_t}}/{varepsilon_s}} {[e^{{-phi_s}/{phi_t}}+{phi_s}/{phi_t}-1]} ({d{phi}}/{dx})^2 = {{2qp_0{phi_t}}/{varepsilon_s}} {[e^{{-phi_s}/{phi_t}}+{phi_s}/{phi_t}-1]}](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_855e8510556e127170a4942ff38012dd.png)
|
![({d{phi}}/{dx})^2 = {{2qp_0{phi_t}}/{varepsilon_s}}{e^{-2{phi_F}/{phi_t}}}{[e^{{phi_s}/{phi_t}}+{phi_s}/{phi_t}-1]} ({d{phi}}/{dx})^2 = {{2qp_0{phi_t}}/{varepsilon_s}}{e^{-2{phi_F}/{phi_t}}}{[e^{{phi_s}/{phi_t}}+{phi_s}/{phi_t}-1]}](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_0c963a4fa0ab6f89f2ec907f1615395c.png)
|
![({d{phi}}/{dx})^2 = {{2qN_A}/{varepsilon_s}}{[{phi_t}e^{{-phi_s}/{phi_t}}+{phi_s}-{phi_t}]} ({d{phi}}/{dx})^2 = {{2qN_A}/{varepsilon_s}}{[{phi_t}e^{{-phi_s}/{phi_t}}+{phi_s}-{phi_t}]}](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_b0b4905bb777111f0fec1b568960e0c6.png)
|
![({d{phi}}/{dx})^2 = {{2qN_A}/{varepsilon_s}}{e^{-2{phi_F}/{phi_t}}}{[{phi_t}e^{{phi_s}/{phi_t}}+{phi_s}-{phi_t}]} ({d{phi}}/{dx})^2 = {{2qN_A}/{varepsilon_s}}{e^{-2{phi_F}/{phi_t}}}{[{phi_t}e^{{phi_s}/{phi_t}}+{phi_s}-{phi_t}]}](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_1770c4582955614032598f221c1e8294.png)
|
 Identity Table
Identity Table
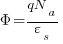
|
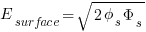
|
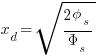
|
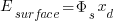 |
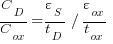
|
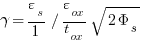 |

0 Comments