Proof: If the sum of the digits of a number is divisible by 3 then the number is divisible by 3

Given a number with digits of the form

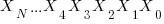
If the sum of these digits is equal to a number that is divisible by 3 then the number is divisible by 3.  Proof follows

Starting wi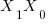th      with 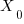 which must be 0.3,6,9 then  

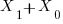   is said to be divisible by 3 thus  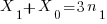   Where 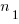 is an integer

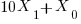       should be divisible by 3.

  Rearranging the terms of 

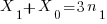
Yields

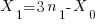
Substituting in 

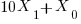
Yields

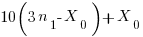
Simplifying yields

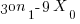
And therefore it is a sufficient condition that if 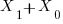 be divisible by 3 then  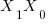  is divisible by 3 and by extension  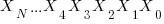 is divisible by 3 if  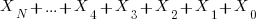 is divisible by 3.

As you might guess the same applies to all powers of 3 with 9 being the most useful next integer.