Research LInks
Find the solution for the system of equations:
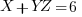 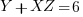 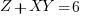
|
Multiply each equation by the term missing to make each second term a triple
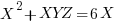
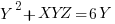
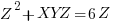
So now subtract the second equation from the first:
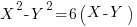
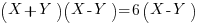
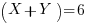
Since the equations are symmetric we should have
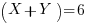
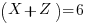
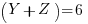
Subtracting the 3rd from the 1st:
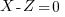 or
or
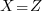 and again since the equations are symmetric
and again since the equations are symmetric 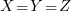
—————
The very first equation at the top 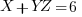 becomes
becomes
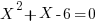
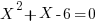
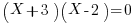 giving the solutions
giving the solutions
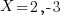
0 Comments