MOSFET Threshold Voltage Formula Derivation
At threshold voltage Vt the surface potential is
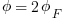
Given this condition threshold voltage is:
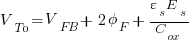 ….the 3rd term is V=Q/C
….the 3rd term is V=Q/C
Reorganizing terms:
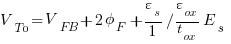
Substituting the identity for Es:
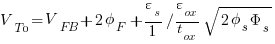
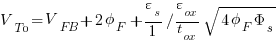
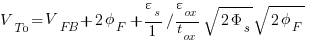
Substituting for the body effect factor identity gamma:
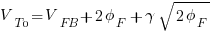
….this is the same as equation 2.1.63 of CMOS Analog Design Using All Region MOSFET Modeling
Equation 2.1.59 can be found in: Tsividis:Operation and Modeling of the MOS Transistor :Page 110
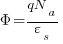
|
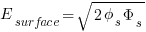
|
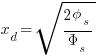
|
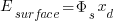 |
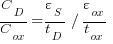
|
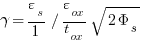
|
Research Links
