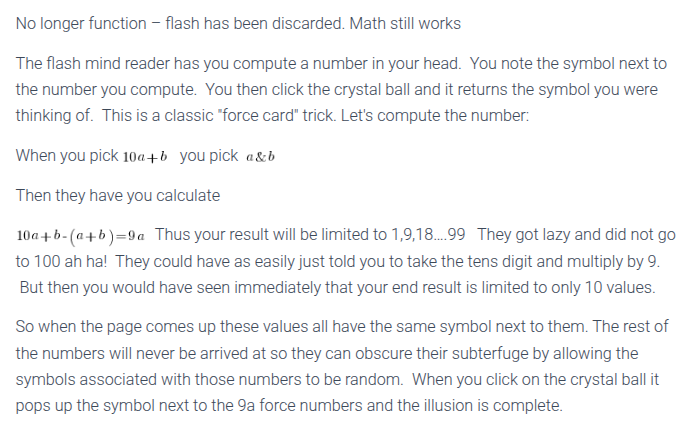
Math
Eulers Theorem
If you followed the proof for Fermat's little theorem then you can understand this generalization rapidly. As before when the integer a is coprime to p you get the jumble of all the integers 1,2,3…p-1. This was guaranteed by p being prime in Fermat's little theorem. When you relent on that condition then you have some integers a that are not coprime to p and they will not give you a full contingent of integers. See the spread sheet clips below
2 is coprime to 15 and thus all values 0 through 14 are cycled through. 3 is not coprime to 15 and thus the gearing does not cycle through all values.
Math
Euler Fermat Theorem – Fermats Little Theorem
Research Links
- Fermat–Euler theorem
- Euler's totient function
- Fermat's little theorem
- Proofs of Fermat's little theorem
- Proof of Fermat's Little Theorem
- Chinese remainder theorem
- Eulers Theorem – a more general version that only specifies coprime requirement instead of prime requirement.