MOSFET Body Effect Factor – Substrate Bias Effects
- The source and body may not be at the same potential. The curve represented as EFi is the Fermi level from the p substrate through the reverse biased source–substrate junction to the source contact.
- The space charge region width under the oxide increases from the original xd @ threshold value when a VSB > 0 is applied. Since the maximum depletion region depth Xd was due to 2Ef it is now due to 2Ef + Vsb and the maximum Xd is bigger before Vt is reached.
@Threshold with:
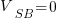
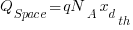
With Vsb applied

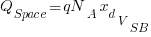
And thus
![Delta Q_Space = qN_A [ x_d_V_SB - x_d_th ] Delta Q_Space = qN_A [ x_d_V_SB - x_d_th ]](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_974.5_8b8c27bbb93afd807efda85f07c514f3.png)

Substituting from the identity table below:
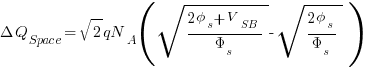
Factoring
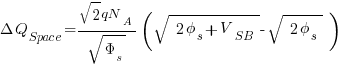
The change in the threshold voltage is
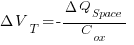
![Delta V_T = {{sqrt{2}}{qN_A }}/{C_ox circ sqrt { Phi_s }}[sqrt { 2 phi_s + V_SB } - sqrt { 2 phi_s } ] Delta V_T = {{sqrt{2}}{qN_A }}/{C_ox circ sqrt { Phi_s }}[sqrt { 2 phi_s + V_SB } - sqrt { 2 phi_s } ]](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_969_bd0cbbdd18b664085b1c0aa1a9391919.png)
And here we find the body effect factor. It is defined as:

The following is my work and needs to be verified
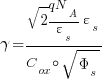
Substituting Identity
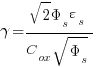
Since:
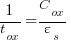
The following simple expression results

Identity Table
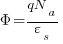
|
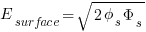
|
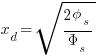
|
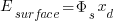 |
Research Links
- Introduction to Solid State Devices: Chapter 10 See page 6, Substrate Bias & Body Effect coefficient page 49 ( The whole book is here )
- PHP Math Publisher Syntax

You have achieved V-pinch off.