Gauss’s Law

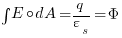[pmath] int{}{}{E circ  dA} = q/ varepsilon_s =Phi [/pmath]   This is the electric field flux

With a uniform charge density that is much more wide and long than it is thick you can use the following:

[pmath] E circ A = q_total / varepsilon_s [/pmath]

[pmath] E circ A = -{qN_a Ax}/{varepsilon_s} [/pmath]

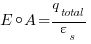
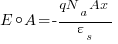
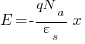[pmath] E = -{qN_a / varepsilon_s} x [/pmath]    So as you progress upwards from 0 the flux increases.

[pmath] d{phi} / dx = -E [/pmath]

[pmath] int{}{}{d{phi}/{dx}} = {qN_a}/{varepsilon_s} {int{0}{x_d}{x}} [/pmath]

[pmath] {phi_s} = {{qN_a}/{varepsilon_s}}  {{x_d}^2}/2 [/pmath]

[pmath] {2 phi_s varepsilon_s}/{qN_a}  = {x_d}^2 [/pmath]

[pmath]  x_d = sqrt {{2 phi_s varepsilon_s}/{qN_a}} [/pmath]

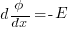
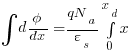
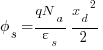
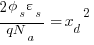
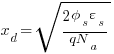
Gathering up terms and using Gauss’s law:

[pmath] Phi = {qN_a / varepsilon_s} [/pmath]

[pmath]  x_d = sqrt {{2 phi_s}/{Phi_s}} [/pmath]

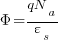
Now that we have the estimate for the depletion width Xd:

[pmath] E_surface = {qN_a / varepsilon_s} x_d [/pmath]

[pmath] E_surface = {qN_a / varepsilon_s}{sqrt{{2 phi_s varepsilon_s}/{qN_a}}} [/pmath]

[pmath] E_surface = sqrt {{2 phi_s qN_a}/{varepsilon_s}} [/pmath]

[pmath] E_surface = sqrt{{2 phi_s Phi_s}} [/pmath]

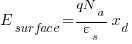
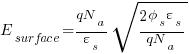
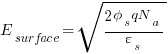
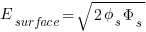
Now the total charge is

[pmath] Q_total = {varepsilon_s} E_surface = {varepsilon_s} {sqrt{{{2 phi_s}{Phi_s}}}} [/pmath]

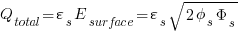
Summary

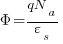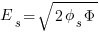
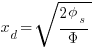
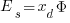
[pmath] Phi = {qN_a / varepsilon_s} [/pmath] Planar Flux Density [pmath] E_s = sqrt { {2 phi_s Phi} } [/pmath]
[pmath]  x_d = sqrt { {2 phi_s } / {Phi} } [/pmath] [pmath] E_s = {x_d} {Phi}[/pmath]

See equation: A2.1.13: CMOS Analog Design Using All Region MOSFET Modeling

Research Links

Gauss’s Law
Introduction to Solid State Devices: Chapter 10   See page 6, Body Effect coefficient page 49