Linear-System-Theory

Sage: Open Source Mathematics Software System

Sage is a free open-source mathematics software system licensed under the GPL. It builds on top of many existing open-source packages: NumPy, SciPy, matplotlib, Sympy, Maxima, GAP, FLINT, R and many more. 
Access their combined power through a common, Python-based language or directly via interfaces or wrappers. → Tour, Tutorial, Documentation
Mission: Creating a viable free open source alternative to Magma, Maple, Mathematica and Matlab.

 

Research Links

By Fudgy McFarlen, ago

LTSPICE NetList

I want LTSPICE or otherwise to put out a spice deck like netlist as shown in the photo inset and the video embedded below. 

 I have not yet found a way to get this type of output.  All the output formats you can select for export in LTSPICE have the form:

Node#1

RefDes1.Pin1, RefDes2.Pin1 …….

Node#2

RefDes1.Pin2

Which of course is suited to pcb layout programs but not what I am trying to do.   See ExpressPCB Netlist format.

Research Links

By Fudgy McFarlen, ago

Economist and Economic Modeller Steve Keen showing instability inherent in high debt economies

Steve Keen talks about instability inherent in high debt economies.  He does this while modeling economies on a computer and demonstrating the oscillations.

Video Notes

  • I have seen this kind of stability analysis applied before.  It is valid for circuits and system functions – I would posit it is valid for economic systems
  • When economies start using debt to drive employment things are ok for a few economic cycles – then you hit a last cycle when debt taken on is huge – the economic levitation ends – the economy shuts down.
  • The blue trace with loops is a tracing of oscillator "squegging" as we call it in electrical engineering – parametric modulation
  • because private debt levels are so high private deleveraging can overwhelm government deficit spending
  • writing off the bad debt – a.k.a. recognizing the bad debt is the only solution
  • to stabilize the system the system should be tweaked to limit the amount of personal debt individuals are willing to take on – base housing loan prices on rents you can get for said house instead of what appraisers conjure up
  • Full talk at the Whitlam Institute is here
  • The associated PowerPoint presentation is here
By Fudgy McFarlen, ago

Convolution of time signals using polynomials-The Super Easy Z transform

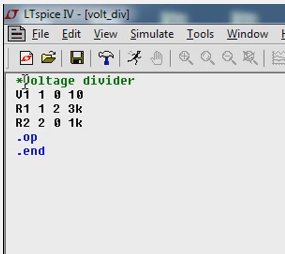
[pmath] 1+x+x^2 [/pmath] [pmath size=16] * [/pmath]   [pmath]  1+x+x^2 = [/pmath]  [pmath]1+2x+3x^2+2x^3+x^4[/pmath]

  • The filter is the sum of the last 3 signal samples. 
  • The signal is a pulse set of three ones.  The signal arrives 1 sample at a time.

Polynomial convolution diagram showing how coefficient of multiplied polynomials correspond to signal amplitudes

Notice the coefficients of the multiplied polynomials are equal to the signal output values at times 0 through 4.

If instead of using X as our variable we could use Z and we would see that all this is the Z transform.   The following principle is true for the above signal and filter.  It is true in general.

    Signal convolved with Filter    [pmath] doubleleftright [/pmath] Transform of signal [pmath size=16] * [/pmath]  Transform of filter

Notice that the powers of X perform the function of place holding for location in time.  They keep track of what we can tally and these tallies correspond in power of X to time.  Time=4 corresponds to powers of 4 of X.

By Fudgy McFarlen, ago