Math
Intersecting Chord Theorem
This video sets out a puzzle that uses the intersecting chord theorem to solve.
Which led me to a couple of basic geometric properties that I did not explicitly know.
Computing
Vigenere Cipher And Breaking it
This code was originally thought to be unbreakable. You use a key such as PASSWORD. Each Letter in your message is encoded by placing
PASSWORDPASSWORDPASSWORD
THISISATESTOFTHECODE
Each letter is encoded by selecting the corresponding column from the key letter above your message letter. The obvious failing is that after a bit you run out of key and start repeating. This makes the code subject to frequency analysis. Of course if your key word is a phrase of some length you might be able to avoid that.
It is interesting that only about 150 years ago this would be considered unbreakable.
![300px-vigenc3a8re_square_shading[1]](http://www.amarketplaceofideas.com/wp-content/uploads/2015/09/300px-vigenc3a8re_square_shading1.jpg)
Research Links
- Vigenère cipher
- Why is Vigenere so strong?
- Vigenere cracking tool – interesting page that lets you see the role letter frequency plays. If you read this far you should go play with this.
Physics
Summary Outline of Richard Feynmans Thesis – Framework for learning QED and Quantum Mechanics in general
He was a fun guy.
A reasonable strategy for learning QED would be to try to recreate Richard Feynman's path of discovery that lead him to his thesis paper. If you are an electrical or computer engineer you should probably set about the task of learning the subject for sooner or later quantum computing and nanotechnology are going to go mainstream. If I am successful in learning this subject it will mark the first time I have not been at least 10 years behind the technology curve when it finally hits.
Research Links
— The following summary is from his Nobel prize address in 1965 and yields some insight as to how he went about the problem of reformulating QED into a more usable form. It includes some information about the wrong turns he took which of course is very instructive in and of itself. —
Math
Long hand division generation of polynomials
Do a long hand division of [pmath] 1/{1-x} [/pmath]
x greater than or equal to 1 does not result in convergence of this sum. However this algorithm can still be used to do some interesting things. Let us use a complex value of [pmath] x = .707+.707i [/pmath]
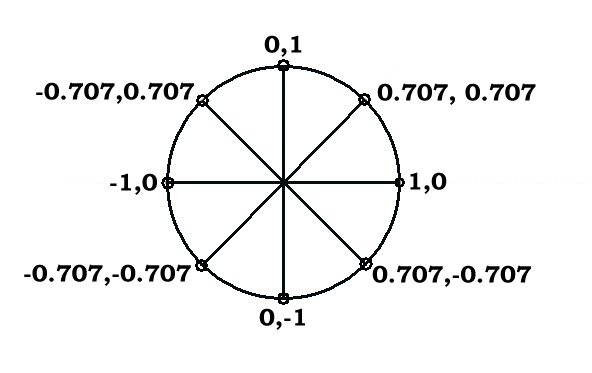
Each power of x yields a result one step around this unit circle. Thus this series is the Z transform of the associated sequence. [1,0] , [0.707,0.707] , [0,1] ……. This sequence is [pmath] Sin( (n-1)*pi/{4}) [/pmath]
Thus the z transform of this sequence is: [pmath] 1/{1-(0.707+0.707i)*x} [/pmath]
If you want to get express in terms of n instead of n-1 you can multiply by 1/x. Since x is the place holder it is easy to see if you want to slide a series one unit to the left by dividing by x.
[pmath] Sin( n*pi/{4}) [/pmath] : note this series starts at 45 degrees phase!
More information:
Math
Z transform of and exponentially decaying sequence
The series: [pmath] x^n [/pmath] [pmath]doubleleftright[/pmath] [pmath]1+ x + x^2 + x^3 + …. = 1/{1-x} n=0,1,2… [/pmath] this converges for x < 1 : Both of these expressions are the Z transform of the [pmath] x^n [/pmath] exponential decay sequence. The first expression is easier to deal with because it is smaller and easier to work with. The following diagram uses a decay sequence with [pmath] x = 0.75 [/pmath]
The filter takes what ever input it is fed and every interval multiplies it by 0.75. To see the filters time response you can thus feed in a single ping. This results in the filter output tracing out a special response. This is called the impulse response. It is the same as the filter plot above.
The exponential decay is maximum entropy. That is to say this is how concentrated things soak out into the rest of the world as they become more dilute.