Long hand division generation of polynomials

Do a long hand division of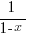  

x greater than or equal to 1 does not result in convergence of this sum.  However this algorithm can still be used to do some interesting things.  Let us use a complex value of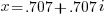   

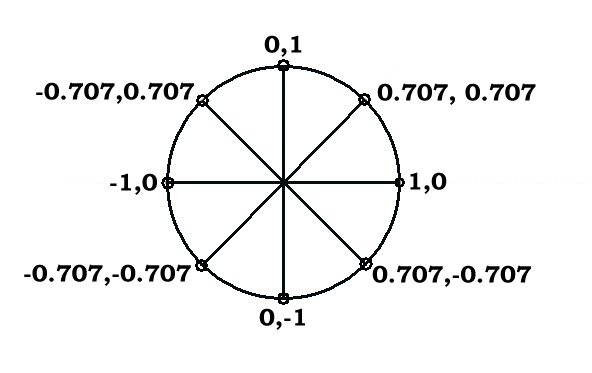
Each power of x yields a result one step around this unit circle. Thus this series is the Z transform of the associated sequence.  [1,0] , [0.707,0.707] , [0,1] ……. This sequence is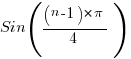  

Thus the z transform of this sequence is: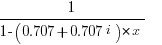    

If you want to get express in terms of n instead of n-1 you can multiply by 1/x.  Since x is the place holder it is easy to see if you want to slide a series one unit to the left by dividing by x. 

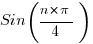   : note this series starts at 45 degrees phase!

More information:

• Generating Functions
• Z Transform