Physics

Conversion of Optical Photons into Electrical Photons as might occur in a battery

See previous post on how a battery and electrical condustors work.  In that post it describes a process in which a visible light photon is generated inside a battery by the 1.5 volt chemical reaction.    I was curious when I wrote that how the optical photon could be converted to an electrical photon.  The above diagram gives a possible explanation how that could occur. When you have an optical photon generated inside of an opaque material it can not propagate very far.   It forms a region with increased photonic pressure.   It is absorbed at some high level excited state of a charge carrier.  It then can cascade downwards in the small steps of the conduction band.  This allows the energy to propagate along the copper in the form of electrical current.

You can also imagine a solar cell acting in a similar fashion with the source of the optical photon being sunlight instead of chemical energy of the battery.

By Fudgy McFarlen, ago

How do electrical conductors work?

My previous inquiry into how batteries work to produce power lead me to a new question:

    How does the power produced in a battery propagate along a copper wire conductor when the 1.5 volt battery potential yields a visible light photon that is known NOT to propagate in a metal?

The following auxiliary questions arise and are answered by the above

-1- What is "DC" current?   ………  DC is a reservoir of electrons transitioning from the higher energy state to the lower and supplying the "bump" a photon supplies to the load.

-2- Why is high voltage more efficient use of power for long distance transmission?  Lower "current" is equal to saying "lower rate of electron transition which means less interaction with the elements of the lattice.  Each interaction carries a probability of bleeding off some of the energy as heat.

-3- what is voltage and current as classically used terminology? Voltage is the same as classically described.   Current is not really a flow of charge past a point but rather the rate of energy level transitions at that point

 

The probability of transition from valence band to conduction band goes down with increasing energy gap.  Why does this affect conduction?  See the next diagram.  The circles are base states of electrons. The figure eights are the first excited state of an electron.  These states are used in a representative fashion to depict relative energy levels and should not be interpreted too literally.

\

Observations

  • A conductor or semiconductor sets up a wave guide for the propagation of a photon
  • In a semiconductor the photon must be the result of a 0.7 volt electron volt potential drop more or less to exceed waveguide cutoff frequency
  • In a conductor there is no forbidden band due to the conduction and valence band overlapping.  Thus waveguide cutoff frequency is more or less 0 hertz   
By Fudgy McFarlen, ago

Physics and chemistry of a dry cell battery

 Outer layer: Zinc                           Middle layer: Ammonium Chloride                       Inner layer: Manganese Dioxide                       Carbon Rod            WaveGuide(wire)

Zn(s) → Zn2+(aq) + 2 e-  U+2192.svg         2 e-  + 2NH4+(aq) → 2NH3(aq) +  H2(g)   U+2192.svg    H2(g) +  2MnO2(s)→ Mn2O3(s) + H2O(l)   U+2192.svg       2e-         U+21E5.gif          Photon

                                    U+2190.gif2Cl         

My original thinking

Without a waveguide aka "wire going to load completing the circuit" charge builds up so as to impede the zinc + chlorine reaction.  That is to say the energy state of the electrons on or about the carbon rod are same state as those emanating from the zinc + chlorine reaction. That leaves new movers no where to go.  When the wave guide path is completed the electrons are able to accelerate and thereby to emit a photon and depopulate the state allowing more electrons to follow it on the path it has just taken.  The photon skips down the waveguide at near the speed of light with intermittent interactions with the conductor.  This can be visualized like a stone skipping across water as can be done with a flat rock across the surface of a pond.  The points where the rock touches the water are the interactions with conductor.  Remember this occurs as a push pull affair.  While the electronic force pushes out the carbon rod it pulls in the cathode. This is standard waveguide behavior which an RF engineer would call paired currents The propagation of which is the photon itself. This is an informatic transfer in that time is required for the energy to propagate as opposed to a book keeping like transfer that occurs with entanglement.  

Next Question:  What is the frequency of the photon involved in transfer of e- charge over a potential of 1.5 volts?

1 electron volt = 1.60217646 × 10-19 joules

Planck's constant = 6.626068 × 10-34 m2 kg / s

E=hF

…but this leads to a crazy high value computed for frequency of the photon???

F=386 Terrahertz????   What am I doing wrong?  Am I doing anything wrong?     Visible light spans 400–790 THz.   This part makes sense if one thinks about an light emitting diode (LED).   That is the reverse.  Electricity travels down a wire and is turned into visible photons in this frequency range.

At this point I panic because I know that this frequency does not propagate well along a wire wave guide as described above or at least right now so I think.  Is there a frequency conversion mechanism?  Seems there must be.  Unless there is some sort of group phenomena.   If one thinks and realizes that "DC" current is made up of photons then DC is made out of a fundamentally AC phenomena namely photons. 

Heuristic notes:  

  1. Imagine a 1400Mhz oscillator.  The waves propagating out from it are very much lower in frequency than the frequency of the photon in the above calculations.  Yet I can easily measure a wave that has 2 volts peak to peak amplitude. 
  2. How does group behavior relate to this?  Can visible light photons be propagated in the belly of a wave group that is much slower?

Answers to the questions generated by this post

  1. How optical photons are converted to low frequency photons for transport along copper wire waveguide
  2. How do electrical conductors work?

Background Information

Chemical reactions (following from wikipedia )

From Zinc Carbon Battery: In a zinc-carbon dry cell, the outer zinc container is the negative terminal. The zinc is oxidised according to the following half-equation.

    Zn(s) → Zn2+(aq) + 2 e-

A graphite rod surrounded by a powder containing manganese(IV) oxide is the positive terminal. The manganese dioxide is mixed with carbon powder to increase the electrical conductivity. The reaction is as follows:

    2MnO2(s) + H2(g)→ Mn2O3(s) + H2O(l)

The H2 comes from the NH4+(aq):

    2NH4+(aq) + 2 e- → H2(g) + 2NH3(aq)

and the NH3 combines with the Zn2+.   In this half-reaction, the manganese is reduced from an oxidation state of (+4) to (+3).  There are other possible side-reactions, but the overall reaction in a zinc-carbon cell can be represented as:

    Zn(s) + 2MnO2(s) + 2NH4+(aq) → Mn2O3(s) + Zn(NH3)22+(aq) + H2O(l)

The battery has an e.m.f. of about 1.5 V. The approximate nature of the e.m.f is related to the complexity of the cathode reaction. The anode (zinc) reaction is comparatively simple with a known potential. Side reactions and depletion of the active chemicals increases the internal resistance of the battery, and this causes the e.m.f. to drop.  Although carbon is an important element of the battery's composition, it takes no part in the electrochemical reaction, instead only serving to collect current and reduce the resistance of the manganese dioxide mix.

Construction

The container of the zinc-carbon dry cell is a zinc can. This contains a layer of NH4Cl with ZnCl2 aqueous paste separated by a paper layer from a mixture of powdered carbon & manganese (IV) oxide (MnO2) which is packed around a carbon rod.

By Fudgy McFarlen, ago

Quantum entanglement is not as out of the ordinary as you might think

Simplification using single particle experiment explanations

Consider a single particle source.  The particle is equally likely to emit in any direction.  That situation is depicted below
   

What you imagine is that a localized particle emanates from the emitter and you detect it somewhere on your ring of detectors surrounding your experimental set up.  You can use your detectors ringing the emitter to verify that emissions are equally probable at any angle.   I imagine the situation differently.  What I imagine is below:

 
The concentric blue rings depict the phase waves of de broglie  propagating outwards from the emitter. They have no preference in direction.  They propagate in all directions.   When they encounter the ring of detectors one of the detectors detects the particle.   Now something has to prevent all the other detectors from firing and saying they also have detected the particle.  This would violate conservation of energy and what ever other conservation laws.  This is the "collapse" into the measured state above.

Note that this "communication" or universal book keeping function occurs in similar method as entanglement experiments show.  The instant the particle interacts with one detector all other detectors are prohibited from detecting the instant the particle is detected.  An instantaneous non communication book keeping function occurs just like described in polarized entangled photon experiments.   

This thought experiment reduces thinking about entanglement to how the universe uses book keeping functions across space to maintain conservation laws.   Let us apply this to the double slit experiment.   Most explanations of the double slit experiment leave you with the paradox of saying "It looks like 1 particle went through both slits".  Where as the two slit experiment possibly demonstrates the book keeping aspect.

Two entangle Photons

What about the case of 2 entangle photons?   They are created coherently and are assumed identical and indistinguishable.   Their phase waves travel out concentrically and totally overlapping as shown above in the second diagram.   The book keeping rules can not discern if it is received photon number 1 or photon number 2.   In fact it is even meaningless to talk about photon number 1 and 2.  They are identical in every way.  Thus the results of 1 hitting the detector are no different from 2 hitting the detector.  Thus what you measure for 1 is what you will measure for 2.   The book keeping detectors first detect one photon then the second.   Since the book keeping conservations laws govern the detection of the second photon they must see a redundant identical measurement with same instantaneous resolution.  The mechanism is the book keeping principles this resolution occurs instantaneously instead of propagating at the speed of light.  It is only after detection measurement that the "particle" is localized.  Conservation book keeping forces this localization.  

Why does quantum computing appear to be able to do something standard computing based on thermodynamic electronics can not ?

What is the reason for quantum computing being able to do more than classical thermodynamic computing? Quantum computing harnesses physical conservation laws that we have up till now not harnesses in regular calculations. These laws do not propagate at the speed of light but rather instantaneously as a conservation law "book keeping" function.

By Fudgy McFarlen, ago

Quantum Entanglement of Photons demonstrated in relatively low cost set up

  • Louis DeBroglie does not get the credit he deserves for original thinking in quantum machanics – DeBroglie thesis paper   – he won the Nobel Prize in 1929 for very good reasons which you will see if you read his thesis paper.
  • I am looking for the single photon counter used in this experimental setup

PowerPoint presentation of experiment Uses an SPCM-APD  ( Single Photon Counting Module – Avalanch Photo Detector )

One of the experimenters

Relatively simple setup uses spontaneous parametric downconversion of photon to create 2 photons that are entangled.  Then these are sent to 2 single photon detectors.   If you have any of the parts or pieces of this setup for sale I would be interested in buying.     

By Fudgy McFarlen, ago

Summary Outline of Richard Feynmans Thesis – Framework for learning QED and Quantum Mechanics in general

He was a fun guy.

 A reasonable strategy for learning QED would be to try to recreate Richard Feynman's path of discovery that lead him to his thesis paper.   If you are an electrical or computer engineer you should probably set about the task of learning the subject for sooner or later quantum computing and nanotechnology are going to go mainstream.  If I am successful in learning this subject it will mark the first time I have not been at least 10 years behind the technology curve when it finally hits.

Research Links

— The following summary is from his Nobel prize address in 1965 and yields some insight as to how he went about the problem of reformulating QED into a more usable form.   It includes some information about the wrong turns he took which of course is very instructive in and of itself. —

By Fudgy McFarlen, ago

My Guide to all things Richard Feynman

Wikipedia entry  – with a list of papers at the bottom.

Selected papers of Richard Feynman

Feynman related book bit torrents  – includes the Feynman lectures on physics 1, 2, 3 –  Buy a hard copy because they are great but when traveling soft copy is the way to go.

Feynman lectures on computation  – hard copy on Amazon – Bittorrent   – Of course, we might get useful ideas from studying how the brain works, but we must remember that automobiles do not have legs like cheetahs nor do airplanes flap their wings!

By Fudgy McFarlen, ago

Video: KITP Lecture : Putting Weirdness to Work: Quantum Information Science

boxes and soxes

Backup copy: Putting quantum weirdness to work: Quantum Information Science

Quantum physics, information theory, and computer science are among the crowning intellectual achievements of the 20th century. Now, a new synthesis of these themes is underway. The emerg- ing field of quantum information science is providing important insights into fundamental issues at the interface of computation and physical science, and may guide the way to revolutionary technological advances. The quantum laws that govern atoms and other tiny objects differ radically from the classical laws that govern our ordinary experience. In particular, quantum information (information en- coded in a quantum system) has weird properties that contrast sharply with the familiar properties of classical information. Physicists, who for many years have relished this weirdness, have begun to recognize in recent years that we can put the weirdness to work: There are tasks involving the acquisition, transmission, and processing of information that are achievable in principle because Nature is quantum mechanical, but that would be impossible in a less weird classical world. John Preskill will describe the properties of quantum bits ("qubits"), the indivisible units of quantum infor- mation, and explain the essential ways in which qubits differ from classical bits. For one thing, it is impossible to read or copy the state of a qubit without disturbing it. This property is the basis of "quantum cryptography," wherein the privacy of secret information can be founded on principles of fundamental physics. Qubits can be "entangled" with one another. This means that the qubits can exhibit subtle quantum correlations that have no classical analogue; roughly speaking, when two qubits are en- tangled, their joint state is more definite than the state of either qubit by itself. Because of quantum entanglement, a vast amount of classical information would be needed to describe completely the quantum state of just a few hundred qubits. Therefore, a "quantum computer" operating on just a few hundred qubits could perform tasks that ordinary digital computers could not possibly emulate. 

Links

[insert page='quantum-mechanics-table-of-contents-toc' display='content']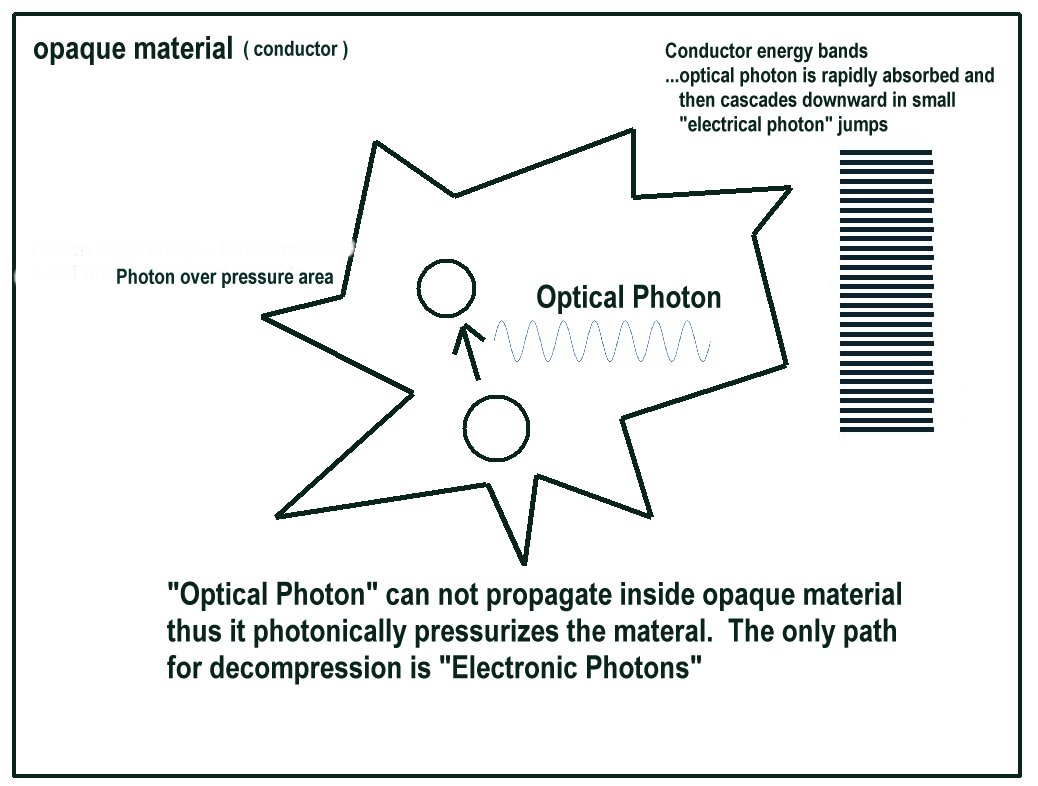
By Fudgy McFarlen, ago