Research Links

• Google: diophantine equation pythagoras
• Chapter 1: DIOPHANTINE ANALYSIS – UnKnown Book
• Diophantine Equations – Chapter 5 –  Diophantine Analysis monograph by Robert Daniel Carmichael

Pythagorean Triples Solution

The square of the odd number

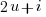    [pmath] 2u+i [/pmath]    is    [pmath] 4u^2+4u+1 [/pmath] 

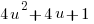
Hence the sum of two odd squares is divisible by 2 but not by 4; and therefore the sum of two odd squares cannot be a square. Hence of the numbers x, y one is even. If we suppose that y is even, then x and z are both odd.

    [pmath] x^2 + y^2 = z^2 [/pmath]    

    [pmath]  y^2 = z^2 – x^2 [/pmath]  

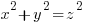
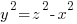
Both x and z terms in the parenthesis below will be odd and thus the sum and difference will be even

    [pmath]  y^2 = ( z – x )( z + x ) [/pmath]

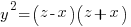
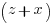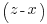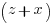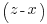Every common divisor of [pmath] ( z + x ) [/pmath]  and   [pmath]  ( z – x ) [/pmath]   is a divisor of their difference 2x. Thence, since z and x are relatively prime odd numbers we conclude that 2 is the greatest common divisor of [pmath] ( z + x ) [/pmath] and [pmath]  ( z – x ) [/pmath] . Then we see that each of these numbers must be twice a square, so that we may write

 [pmath] ( z + x ) =2a^2 [/pmath]    [pmath]  ( z – x )=2b^2 [/pmath]  

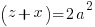
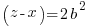
Solving for x, y, z yields

       [pmath] y= 2ab            y=a^2 – b^2          z = a^2 – b^2  [/pmath]    

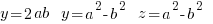
Using values of a & b you can generate all the integer solutions.

---

A variant on the above can be done to illustrate the solution technique more

    [pmath] x^2 + gy^2 = z^2 [/pmath]    

    [pmath]  gy^2 = z^2 – x^2 [/pmath]  

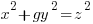
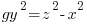
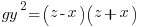    [pmath]  gy^2 = ( z – x )( z + x ) [/pmath]   Using the same argument as above but one of the factors on the right hand side has to account for the g.  Since the g can be in either factor there are two solutions that make up the overall solution

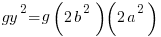    [pmath]  gy^2 = g( 2b^2 )( 2a^2) [/pmath]    Matching the previous phrase with this phrase to equate right hand factor terms

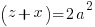
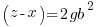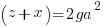
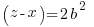
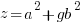
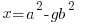  [pmath] ( z + x ) =2a^2 [/pmath]    [pmath]  ( z – x )=2gb^2 [/pmath]      —-OR—-       [pmath] ( z + x ) =2ga^2 [/pmath]    [pmath]  ( z – x )=2b^2     [/pmath] 

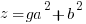
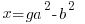
    [pmath]  z = a^2 + gb^2 [/pmath]    [pmath]  x = a^2 – gb^2  [/pmath]      —-OR—-     [pmath]  z  = ga^2 + b^2 [/pmath]    [pmath]  x = ga^2 – b^2  [/pmath] 

Example Solutions with g=2 a=4 b=1
x	y	z	Equation Set
2	4	6	[pmath]  z = a^2 + gb^2 [/pmath][pmath]  x = a^2 – gb^2  [/pmath]
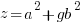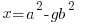
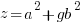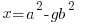
7	4	9	[pmath]  z = a^2 + gb^2 [/pmath][pmath]  x = a^2 – gb^2  [/pmath]