The maximum entropy constraints are as follows:

• Over the interval [0,infinity]
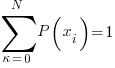•  [pmath size=12] sum{kappa=0}{N}{P(x_i)}=1[/pmath]       …. sum over all probabities must = 1
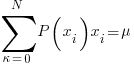•  [pmath size=12] sum{kappa=0}{N}{P(x_i){x_i}}=mu[/pmath]     …. given an average value AKA "mean"

The langrangian is formed as follows:

 [pmath size=12] L=sum{kappa=0}{N}{{-P(x_i)}{log_2 P(x_i)}}+lambda_0(1-sum{kappa=1}{N}{P(x_i)} )+lambda_1(mu-sum{kappa=1}{N}{{P(x_i)}{x_i}})[/pmath]  

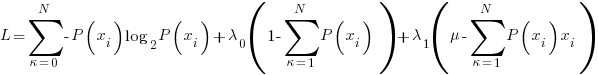
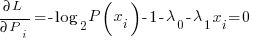 [pmath size=12] {partial L} / {partial P_i}= {-log_2 P(x_i)}-1-lambda_0-lambda_1{x_i}=0[/pmath]    ….setting equal to zero to find the extrema point

 [pmath size=12]{log_2 P(x_i)}=-1-lambda_0-lambda_1{x_i}[/pmath]

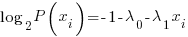
Allowing 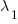 [pmath]{lambda_1}[/pmath] to take up the slack to turn base 2 log into natural log:

 [pmath size=12]{P(x_i)}=e^{-1-lambda_0} e^{-lambda_1{x_i}}[/pmath]

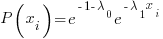
Using the sum of probabilities =1 criteria

 [pmath size=12] sum{kappa=0}{N}{P(x_i)}=e^{-1-lambda_0} {1/{1-e^{-lambda_1}}}=1[/pmath]  

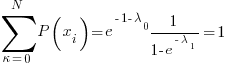
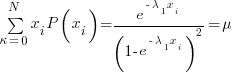 [pmath size=12] sum{kappa=0}{N}{x_i}{P(x_i)}={e^{-lambda_1{x_i}}/(1-e^{-lambda_1{x_i}})^2}={mu}[/pmath]    ( See below for derivation)

 

Derivation of mean value infinite sum:

                 [pmath size=12]sum{kappa=0}{N}{x_i}{e^{-lambda_1{x_i}}}=0+1*e^{-lambda_1}+2*e^{-2{lambda_1}}+3*e^{-3{lambda_1}}cdots[/pmath]  

           [pmath size=12]e^{-lambda_1}{sum{kappa=0}{N}{x_i}{e^{-lambda_1{x_i}}}=………………1*e^{-2{lambda_1}}+2*e^{-3{lambda_1}}+3*e^{-4{lambda_1}}}cdots[/pmath]  

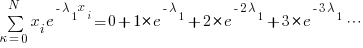
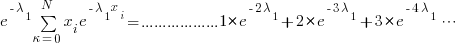
Subtracting we get the same old geometric series that we all know

[pmath size=12](1-e^{-lambda_1{x_i}}){sum{kappa=0}{N}{x_i}{e^{-lambda_1{x_i}}}}=0+1*e^{-lambda_1}+1*e^{-2{lambda_1}}+1*e^{-3{lambda_1}}cdots[/pmath]

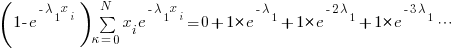
Rearranging terms:

[pmath size=12](1-e^{-lambda_1{x_i}}){sum{kappa=0}{N}{x_i}{e^{-lambda_1{x_i}}}}={e^{-lambda_1{x_i}}/(1-e^{-lambda_1{x_i}})}[/pmath]

[pmath size=12]{sum{kappa=0}{N}{x_i}{e^{-lambda_1{x_i}}}}={e^{-lambda_1{x_i}}/(1-e^{-lambda_1{x_i}})^2}[/pmath]

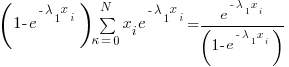
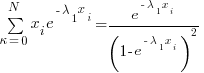
Another way of looking at the series:

Infinite Series Multiplication Table – The product of the 2 series is the sum of all the product entries ad infinitum
[pmath]e^{-3{lambda_1{x_i}}}[/pmath]	[pmath]e^{-3{lambda_1{x_i}}}[/pmath]	…	…	…
[pmath]e^{-2{lambda_1{x_i}}}[/pmath]	[pmath]e^{-2{lambda_1{x_i}}}[/pmath]	[pmath]e^{-3{lambda_1{x_i}}}[/pmath]	…	…
[pmath]e^{-lambda_1{x_i}}[/pmath]	[pmath]e^{-lambda_1{x_i}}[/pmath]	[pmath]e^{-2{lambda_1{x_i}}}[/pmath]	[pmath]e^{-3{lambda_1{x_i}}}[/pmath]	…
[pmath]1[/pmath]	[pmath]1[/pmath]	[pmath]e^{-lambda_1{x_i}}[/pmath]	[pmath]e^{-2{lambda_1{x_i}}}[/pmath]	[pmath]e^{-3{lambda_1{x_i}}}[/pmath]
	[pmath]1[/pmath]	[pmath]e^{-lambda_1{x_i}}[/pmath]	[pmath]e^{-2{lambda_1{x_i}}}[/pmath]	[pmath]e^{-3{lambda_1{x_i}}}[/pmath]

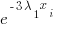
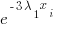
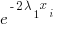
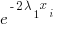
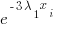
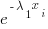
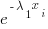
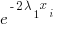
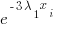
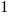
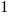
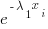
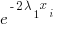
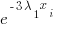
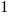
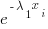
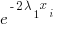
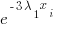
The table uses 2 exponential series each starting with 1.  In order to get the same series as the solution in the derivation above multiple the result by 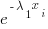[pmath]e^{-lambda_1{x_i}}[/pmath]

It forms a sort of number wedge or number cone. I wonder if it extends to 3 dimensions?

Observations  ( Need to complete this ) 

• ….delay like Z transform
• continuous form correspondence with discrete form

Research Links

• The Exponential Distribution Local copy
• Boltzman's distribution