Research Links

• The Maximum Entropy Principle – The distribution with the maximum entropy is the distribution nature chooses
• Maximum Entropy Distribution for Random Variable of Extent [0,Infinity] and a Mean Value Mu
• Quantum Harmonic Oscillator: Wavefunctions
• Hermite polynomials

 

In many physical systems the question arises what is the probability distribution that describes a system with a given expected energy E  over the interval from -infinity to + infinity?     Again you will use the maximum entropy principle to determine this.

The constraints are as follows:

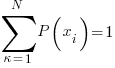•  [pmath size=12] sum{kappa=1}{N}{P(x_i)}=1[/pmath]       …. sum over all probabities must = 1
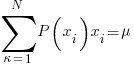•  [pmath size=12] sum{kappa=1}{N}{P(x_i){x_i}}=mu[/pmath]     …. given an average value AKA "mean"
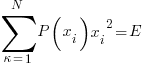•  [pmath size=12] sum{kappa=1}{N}{P(x_i){x_i}^2}=E[/pmath]     ….. given an "energy" or standard deviation AKA "variance"

The langrangian is formed as follows:

 [pmath size=12] L=sum{kappa=1}{N}{{-P(x_i)}{log_2 P(x_i)}}+lambda_0(1-sum{kappa=1}{N}{P(x_i)} )+lambda_1(mu-sum{kappa=1}{N}{{P(x_i)}{x_i}})+lambda_2(E-sum{kappa=1}{N}{{P(x_i)}{x_i}^2})[/pmath]  

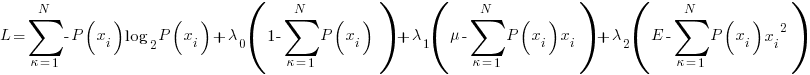
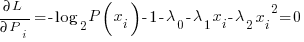 [pmath size=12] {partial L} / {partial P_i}= {-log_2 P(x_i)}-1-lambda_0-lambda_1{x_i}-lambda_2{x_i}^2=0[/pmath]    ….setting equal to zero to find the extrema point

Now the problem is to solve for the lambda coefficients.   I use a trick.  I assume the curve centered at the Y axis.   The curve must have the same amount of entropy on the left side of the Y axis as on the right or entropy will not be maximized.  Because the polynomial is even degree the probability curve must be "even"….that is symmetric about the Y axis.  That reduces the previous langrangian to:

 [pmath size=12] {partial L} / {partial P_i}= {-log_2 P(x_i)}-lambda_2{x_i}^2=0[/pmath] 

 [pmath size=12] {log_2 P(x_i)} = -lambda_2{x_i}^2  [/pmath]

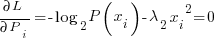
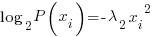
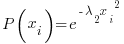 [pmath size=12]  P(x_i) = e^{-lambda_2{x_i}^2}  [/pmath]         …..which you will recognize as the gaussian distribution

 

 

Solve for the coefficients using identity of the integral of normal -infin to + infin

Using the identity and setting it to 1: 

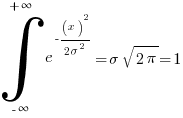[pmath size=12]int{-infty}{+infty}{e^{-{(x)^2/{2sigma^2}}}}=sigma{sqrt{2pi}} =1[/pmath]     yields: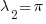  [pmath size=12]lambda_2={pi}[/pmath] 

         The resultant distribution is: 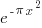     [pmath size=12]{e^{-{pi}x^2}}[/pmath]    which is the normal distribution.

 Now for the other coefficients the job is made easier by observing the distribution can only retain this even about the mean form if  the polynomial is in the form :  (x-mu)^2  : this form can propagate along the X axis without distribution shape change.  Gaussian wave packet can not change shape because it is already max entropy.  If it changes shape it decreases entropy which requires force and increases its energy.  But that would be a change in state which we are assuming is not happening.

 

Observations

• base state of quantum harmonic oscillator is gaussian : It is maximum entropy.  
• gaussian wave packet can not mishapen because it is already max entropy.  If it changes shape it decreases entropy which requires force.
• gaussian is the base state of the wave packet?  Is it possible to have forms of the higher energy states? What would the contraint be to get to the state  [pmath size=12]  psi_1  [/pmath] ?
• It's pretty obvious from physics of antennas and the diagram below that sine waves are maximum entropy also.  What is the set of contraints that yield a sine wave solution?

                  

What about the higher order wave functions?  Can they be generated by the Maximum Entropy method?  Backing out the term required  to find the form required for 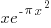[pmath size=12]{ xe^{-{pi}x^2}} [/pmath]  the Lagrangian yields

[pmath size=12] (sum{kappa=1}{N}{{P(x_i)} Log({x_i})  }) [/pmath] 

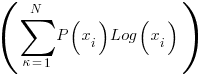
And I do not know why / how that term would occur.