Math
Long hand division generation of polynomials
Do a long hand division of [pmath] 1/{1-x} [/pmath]
x greater than or equal to 1 does not result in convergence of this sum. However this algorithm can still be used to do some interesting things. Let us use a complex value of [pmath] x = .707+.707i [/pmath]
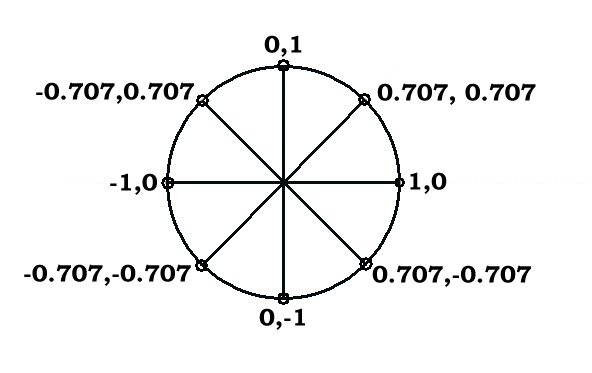
Each power of x yields a result one step around this unit circle. Thus this series is the Z transform of the associated sequence. [1,0] , [0.707,0.707] , [0,1] ……. This sequence is [pmath] Sin( (n-1)*pi/{4}) [/pmath]
Thus the z transform of this sequence is: [pmath] 1/{1-(0.707+0.707i)*x} [/pmath]
If you want to get express in terms of n instead of n-1 you can multiply by 1/x. Since x is the place holder it is easy to see if you want to slide a series one unit to the left by dividing by x.
[pmath] Sin( n*pi/{4}) [/pmath] : note this series starts at 45 degrees phase!
More information:
Math
Z transform of and exponentially decaying sequence
The series: [pmath] x^n [/pmath] [pmath]doubleleftright[/pmath] [pmath]1+ x + x^2 + x^3 + …. = 1/{1-x} n=0,1,2… [/pmath] this converges for x < 1 : Both of these expressions are the Z transform of the [pmath] x^n [/pmath] exponential decay sequence. The first expression is easier to deal with because it is smaller and easier to work with. The following diagram uses a decay sequence with [pmath] x = 0.75 [/pmath]
The filter takes what ever input it is fed and every interval multiplies it by 0.75. To see the filters time response you can thus feed in a single ping. This results in the filter output tracing out a special response. This is called the impulse response. It is the same as the filter plot above.
The exponential decay is maximum entropy. That is to say this is how concentrated things soak out into the rest of the world as they become more dilute.
Math
Two 2 dimensional determinant of a matrix animation showing it is equal to the area of the parallelogram
The 2 dimensional determinant of a matrix can be interpreted as the area of a parallelogram as shown in the following diagram.
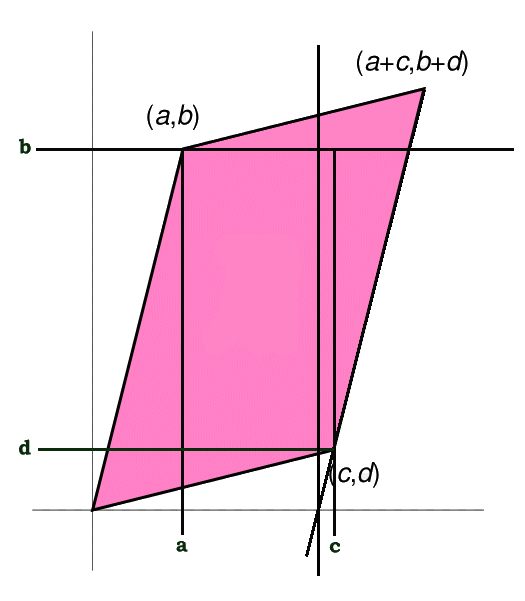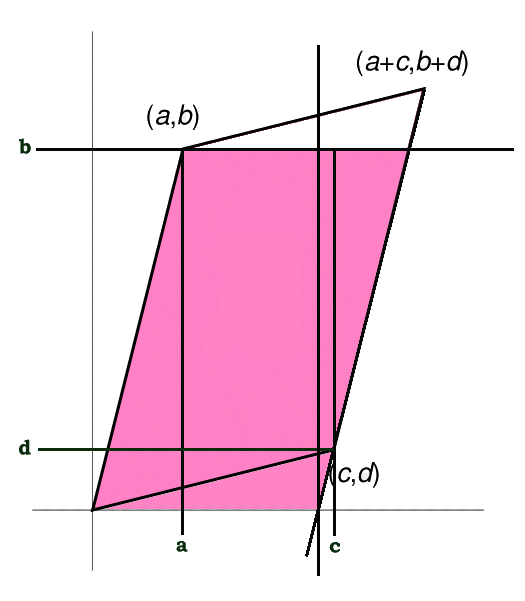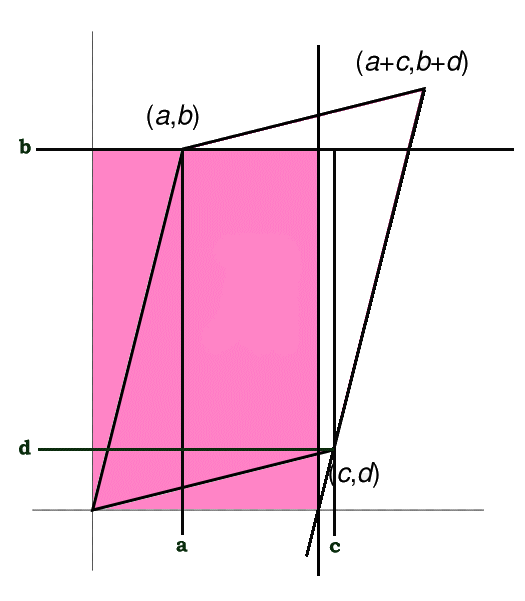
Numeric Example
[pmath] det (matrix{2}{2}{2 1 1 2}) = 2 * 2 – 1 * 1 = 3 [/pmath]
Compare that with the old fashioned area of two triangles that make up the parallelogram:
[pmath] Area Paralelogram = 2 * {1/2} * Base * Height [/pmath]
Using Pythagoras:
[pmath] Height = {3/sqrt{2}} [/pmath]
[pmath] Base = sqrt{2} [/pmath]
[pmath] Area Parallelogram = sqrt{2} * {3/sqrt{2}} = 3 [/pmath]
This carries on through higher dimensions. Below depicts a 3 variable system.
The rows r1, r2, r3 are vectors each. The various summations taken 1, 2 and 3 at a time define a parallelepiped.
The following excerpt is from X and may yield some insight when maximum entropy principle is applied. ( still working on this )
Information-Theory
Derivation of the Normal Gaussian distribution from physical principles – Maximum Entropy
Research Links
- The Maximum Entropy Principle – The distribution with the maximum entropy is the distribution nature chooses
- Maximum Entropy Distribution for Random Variable of Extent [0,Infinity] and a Mean Value Mu
- Quantum Harmonic Oscillator: Wavefunctions
- Hermite polynomials
In many physical systems the question arises what is the probability distribution that describes a system with a given expected energy E over the interval from -infinity to + infinity? Again you will use the maximum entropy principle to determine this.
The constraints are as follows:
Information-Theory
The Maximum Entropy Principle – The distribution with the maximum entropy is the distribution nature chooses
In a previous article entropy was defined as the expected number of bits in a binary number required to enumerate all the outcomes. This was expressed as follows: entropy= H(x)= [pmath size=12] sum{kappa=1}{N}{delim{[}{-P(x_i) * log_2 P(x_i) }{]}}[/pmath] In physics ( nature ) it is found that the probability distribution that Read more…
Information-Theory
Use of Maximum Entropy to explain the form of Energy States of an Electron in a Potential Well
The base state of an electron in an infinite potential well has the most "space" for the electron state. Thus it has the maximum entropy. Take that same state and imagine pinching the electrons existence to nil in the middle of the trough. Now you have state-2. The electron now exists in a smaller entropic state and guess what? It contains exploitable energy now. This is like a spring compressed. The electron can decompress and exert force / expend energy. For example in an interaction with another atom possibly a recoil could occur. In a crystal lattice an electron can transfer its energy to the atom next door and in effect yield conduction. All these are preliminary suppositions subject to more scrutiny. As mentioned before since the electron exists in this potential well in the form of free fall it can not have any acceleration. Thus its distribution must thoroughly avoid the edges of the well were it would indeed experience accelerations by bouncing and recoiling off of the walls.
