Steps

• Derive the value of the square of the voltage on the capacitor
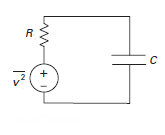
• Assume the noise voltage on the resistor can be faked up and simulated by an equivalent voltage source driving the circuit with a noiseless resistor.  The ideal source is assumed to have uniform power spectral density.
• Equate the value of the voltage on the capacitor with that given by Boltzmann's equipartition theorem and try not to get hanged in the mean time.

Equipartition Theorem: Each orthogonal degree of freedom gets 1/2KT of energy.  This can be thought of as maximum entropy using uniform distribution over each axis. Look for the quadratic energy terms.  With a capacitor all you have is:  [pmath]E_Capacitor={1/2}C{V^2}[/pmath]

[pmath]{1/2}KT={1/2}C{V^2}[/pmath]

[pmath]{KT}/C={V^2}[/pmath]

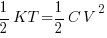
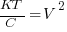
Now the circuit analysis

P.S.D. == Power Spectral Density

PSD(Capacitor Voltage) = PSD(Ideal Voltage Source) * ( Frequency response of the RC circuit )    …….this is in the frequency domain

[pmath]{V_C}^2(f)={{V^2}/{{Delta}{f}}}delim{|}{{1/{{j}{omega}{C}}}/{R+1/{{j}{omega}{C}}}}{|}^2[/pmath]

[pmath]{V_C}^2(f)={{V^2}/{{Delta}{f}}}delim{|}{{1}/{{j}{omega}{R}{C}+1}}{|}^2[/pmath]

[pmath]{V_C}^2(f)={{V^2}/{{Delta}{f}}}{{1}/{({2}{pi}{f}{R}{C})^2+1}}[/pmath]

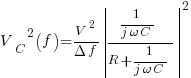
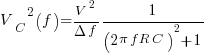
Total energy on the capacitor is the integral [0,infinity]

[pmath]int{0}{+infty}{{V_C}^2(f){df}}={{V^2}/{{Delta}{f}}}int{0}{+infty}{{{1}/{({2}{pi}{f}{R}{C})^2+1}}{df}}[/pmath]      The integral of this is arctan()      

[pmath]{V^2}=int{0}{+infty}{{V_C}^2(f){df}}={{V^2}/{{Delta}{f}}}*{{pi}/{2}}*{{1}/{{2}{pi}{R}{C}}}[/pmath]

The value on the left hand side is the previous value we deduced using Boltzmann:

[pmath]{KT}/C=int{0}{+infty}{{V_C}^2(f){df}}={{V^2}/{{Delta}{f}}}*{{pi}/{2}}*{{1}/{{2}{pi}{R}{C}}}[/pmath]

[pmath]{KT}={{V^2}/{{Delta}{f}}}*{1/{2}}*{{1}/{{2}{R}}}[/pmath]

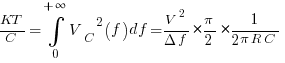
Which yields the relation between noise voltage, bandwidth and resistance.

[pmath]{4}{KT}{R}{{Delta}{f}}={V^2}[/pmath]

Research Links

• Wikipedia: Equipartition Theorem
• Equipartition Theorem: Valance
• Several different approaches to deriving the noise relation including the one taken by Nyquist  – Nyquist approach includes black body radiation concept.
• A brief history of the events leading up to the discovery of thermal noise