- Intuitive Visual Matrices Table of Contents TOC
- Math: Area of a Parallelogram equals geometric mean of triangles
- Math: Derivation of Matrix Determinant
- Two 2 dimensional determinant of a matrix animation showing it is equal to the area of the parallelogram
- Interpretation of Matrix determinant as hyper-volume
- Intuitive Matrix Inverse
- Solution of similtaneous linear equations
- Matrices, Eigenvalues, Eigenvectors
End of TOC
All the explanations of matrix determinant leave out the motive behind the crime. This is the worst thing that can possibly be done as everything flows from that. You can get an idea where the definition of the determinant of a matrix came from by looking at the simplest case of a 2×2 system of equations:
To solve for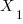 
reduce the b position coefficient to zero
Here is the seed. The solution looks like
Which you should recognize as Cramers rule lurking in the bushes.
Now let us take it a little further. Click into the links below to first see the derivation of the determinant of a 3×3 matrix. Then clink into the derivation of the determinant of a 4×4 matrix and higher with recursion.
Derivations
- Derivation of 3×3 determinant – This is used as a basis to develop notation that is useful in the final proof based on the 4×4 derivation
- Matrix-Determinant.lyx – original document
- Derivation of 4×4 determinant and deriving higher order determinants using recursion
- Matrix-Determinant-4×4-and-higher.lyx – original document
Research Links
0 Comments