The Maximum Entropy Principle – The distribution with the maximum entropy is the distribution nature chooses

In a previous article entropy was defined as the expected number of bits in a binary number required to enumerate all the outcomes.  This was expressed as follows:

entropy= H(x)=  

In physics ( nature ) it is found that the probability distribution that represents a physical process is the one that has the maximum entropy given the constraints on the physical system.   What are constraints?  An example of a probabalistic system is a die with 6 sides.  For now pretend you do not know that it is equally likely to show any 1 of the 6 faces when you roll it.  Assume only that it is balanced.

In the case of a die the above summation is equivalent to the following sort of computation:

• Initial assumption set of 6 probabilities that  sum up = 1  … this is a given as it has to be at least one of the 6 faces unless it stands on edge Twilight Zone style.  Lets assume P(x_i) = 0.05, 0.05, 0.05, 0.05,0.05, 0.75  …. you know instinctively this is not correct but demonstrates the maximum entropy principle

The total entropy given these probabilities = (.05) * (4.322) * 5 + 0.75 * (.415)= 1.0805 + .311= 1.39 bits

Let us use our common sense now.  We know there are 6 equally probable states that can roll up.  So its easy to calculate the number of bits required.  

• Bits required = log₂6 = 2.585 bits 

Thus we can see our initial assumption of probabilities yields an entropy number less than we would expect from common sense.   How do we find the maximum entropy possible? 

• Use the Langrangian maximization method. 
• Maximize the entropy phrase with the constraint that  

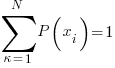                 …. sum over all probabities must = 1

The langrangian is formed as follows:

Now differentiating the langrangian and setting the derivative = 0 we can find the maximal entropic probability

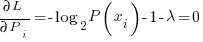
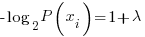         solving for the P_i  yields

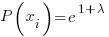        All the P_i= the same constant with the probabilities summing to 1….Thus P_i=1/6 since N=6

While this is alot of work to derive the obvious it there is a purpose. In the case of more complicated situations where the probability distribution is not obvious this method works.  For example in the case of the Black Body emission curve of Planck.  Given just the quantization of energy levels you can derive the black body curve!!  This principle is woven all through nature.  Learn it because it will serve you well. 

Some interesting Notes to myself — myself? I meant me.

• Maximum Entropy Modeling – Local:PDF  –    including some open source software