Derivation of the Normal Gaussian distribution from physical principles

Research Links

In many physical systems the question arises what is the probability distribution that describes a system with a given expected energy E over the interval from -infinity to + infinity? Again you will use the maximum entropy principle to determine this.

The constraints are as follows:

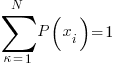$sum{kappa=1}{N}{P(x_i)}=1$ …. sum over all probabities must = 1
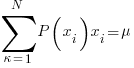$sum{kappa=1}{N}{P(x_i){x_i}}=mu$ …. given an average value AKA "mean"
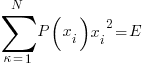$sum{kappa=1}{N}{P(x_i){x_i}^2}=E$ ….. given an "energy" or standard deviation AKA "variance"

The langrangian is formed as follows:

$L=sum{kappa=1}{N}{{-P(x_i)}{log_2 P(x_i)}}+lambda_0(1-sum{kappa=1}{N}{P(x_i)} )+lambda_1(mu-sum{kappa=1}{N}{{P(x_i)}{x_i}})+lambda_2(E-sum{kappa=1}{N}{{P(x_i)}{x_i}^2})$

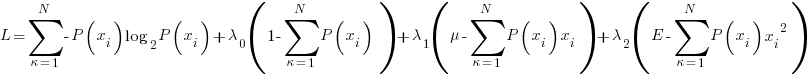
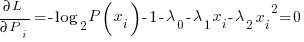${partial L} / {partial P_i}= {-log_2 P(x_i)}-1-lambda_0-lambda_1{x_i}-lambda_2{x_i}^2=0$ ….setting equal to zero to find the extrema point

Now the problem is to solve for the lambda coefficients. I use a trick. I assume the curve centered at the Y axis. The curve must have the same amount of entropy on the left side of the Y axis as on the right or entropy will not be maximized. Because the polynomial is even degree the probability curve must be "even"….that is symmetric about the Y axis. That reduces the previous langrangian to:

${partial L} / {partial P_i}= {-log_2 P(x_i)}-lambda_2{x_i}^2=0$

${log_2 P(x_i)} = -lambda_2{x_i}^2$

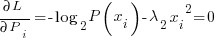
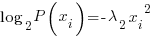
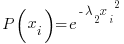$P(x_i) = e^{-lambda_2{x_i}^2}$ …..which you will recognize as the gaussian distribution

Solve for the coefficients using identity of the integral of normal -infin to + infin

Using the identity and setting it to 1:

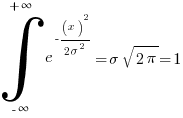$int{-infty}{+infty}{e^{-{(x)^2/{2sigma^2}}}}=sigma{sqrt{2pi}} =1$ yields: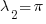 $lambda_2={pi}$

The resultant distribution is: 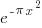${e^{-{pi}x^2}}$ which is the normal distribution.

Now for the other coefficients the job is made easier by observing the distribution can only retain this even about the mean form if the polynomial is in the form : (x-mu)^2 : this form can propagate along the X axis without distribution shape change. Gaussian wave packet can not change shape because it is already max entropy. If it changes shape it decreases entropy which requires force and increases its energy. But that would be a change in state which we are assuming is not happening.

Observations

base state of quantum harmonic oscillator is gaussian : It is maximum entropy.
gaussian wave packet can not mishapen because it is already max entropy. If it changes shape it decreases entropy which requires force.
gaussian is the base state of the wave packet? Is it possible to have forms of the higher energy states? What would the contraint be to get to the state ?
It's pretty obvious from physics of antennas and the diagram below that sine waves are maximum entropy also. What is the set of contraints that yield a sine wave solution?

What about the higher order wave functions? Can they be generated by the Maximum Entropy method? Backing out the term required to find the form required for 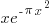${ xe^{-{pi}x^2}}$ the Lagrangian yields

$(sum{kappa=1}{N}{{P(x_i)} Log({x_i}) })$

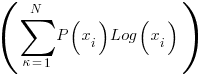
And I do not know why / how that term would occur.

Derivation of the Normal Gaussian distribution from physical principles

Published by Fudgy McFarlen on August 25, 2008August 25, 2008

0 Comments

Leave a Reply