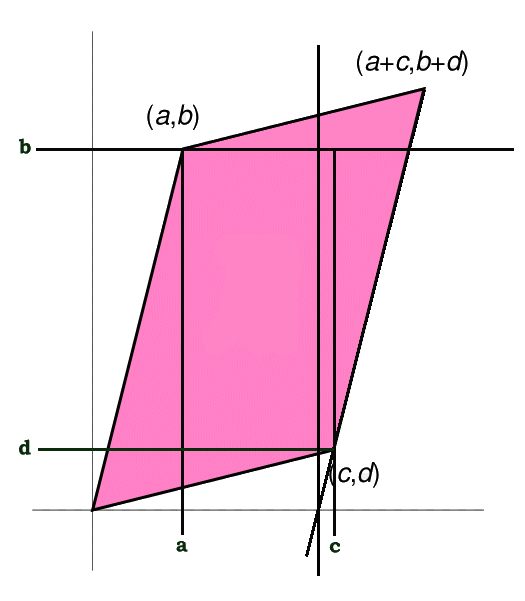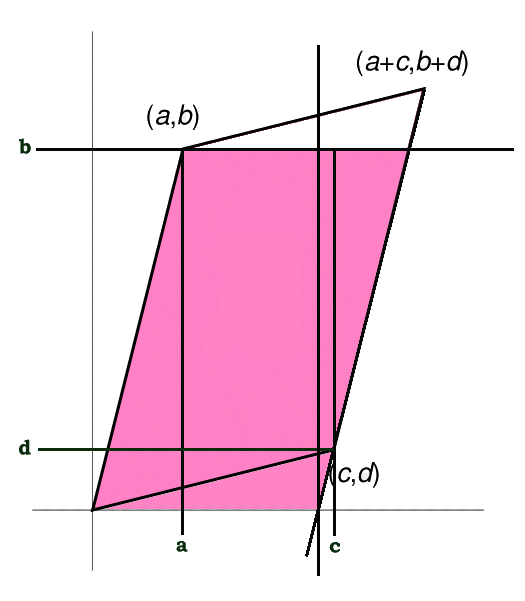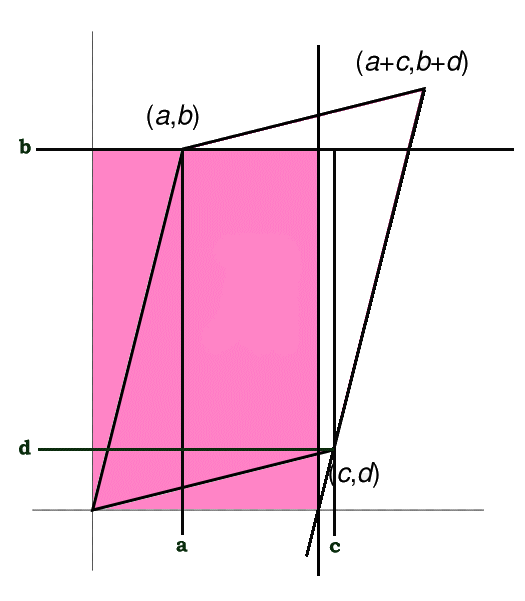David Mermin is great presenter. Emailed him and tried to get him to grade my solution to the homework problem. He did not want to give away the answer and spoil future talks.
This is the story of Dewar and Kamerlingh Onnes race to liquify gases. The ultimate challenge was helium. Dewar gavce up after hydrogen as he found it difficult to get helium and had all along gone light on equipment whilst Onnes used a more industrial approach,. Onnes received the Nobel prize for doing this.
The unfortunate thing is that later superconductivity and superfluidity was found by Onnes. Had Dewar persisted he might have found superconductivity and got the prize anyway!
The ultimate acheivement detailed is the creation of an Bose Einstein condensate in 1995.
If you like science / physics this one is for you!
Simple is good
The reason why is that the entangle states provides greater enumeration. It is as if the bits are conscience of one another. What this video does is better than others is to strip the wave mechanics out of quantum computing to the extent possible.
Explanations are phrased in terms of red and green balls put in boxes with 2 doors. Put a red ball in a box through door number 1 and if you go back and observe the ball through door number 1 it is always red. If you observe the ball through door number 2 then it is 50-50 odds that you observer red or green.
More explanation after I watch a few times.
Do a long hand division of [pmath] 1/{1-x} [/pmath]
x greater than or equal to 1 does not result in convergence of this sum. However this algorithm can still be used to do some interesting things. Let us use a complex value of [pmath] x = .707+.707i [/pmath]
Each power of x yields a result one step around this unit circle. Thus this series is the Z transform of the associated sequence. [1,0] , [0.707,0.707] , [0,1] ……. This sequence is [pmath] Sin( (n-1)*pi/{4}) [/pmath]
Thus the z transform of this sequence is: [pmath] 1/{1-(0.707+0.707i)*x} [/pmath]
If you want to get express in terms of n instead of n-1 you can multiply by 1/x. Since x is the place holder it is easy to see if you want to slide a series one unit to the left by dividing by x.
[pmath] Sin( n*pi/{4}) [/pmath] : note this series starts at 45 degrees phase!
More information:
The series: [pmath] x^n [/pmath] [pmath]doubleleftright[/pmath] [pmath]1+ x + x^2 + x^3 + …. = 1/{1-x} n=0,1,2… [/pmath] this converges for x < 1 : Both of these expressions are the Z transform of the [pmath] x^n [/pmath] exponential decay sequence. The first expression is easier to deal with because it is smaller and easier to work with. The following diagram uses a decay sequence with [pmath] x = 0.75 [/pmath]
The filter takes what ever input it is fed and every interval multiplies it by 0.75. To see the filters time response you can thus feed in a single ping. This results in the filter output tracing out a special response. This is called the impulse response. It is the same as the filter plot above.
The exponential decay is maximum entropy. That is to say this is how concentrated things soak out into the rest of the world as they become more dilute.
The 2 dimensional determinant of a matrix can be interpreted as the area of a parallelogram as shown in the following diagram.
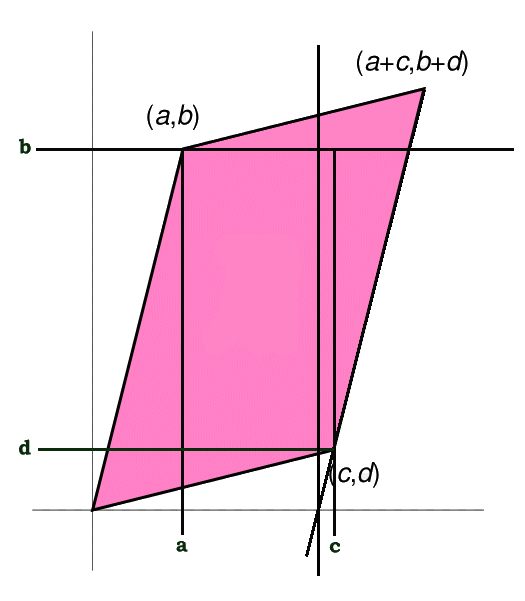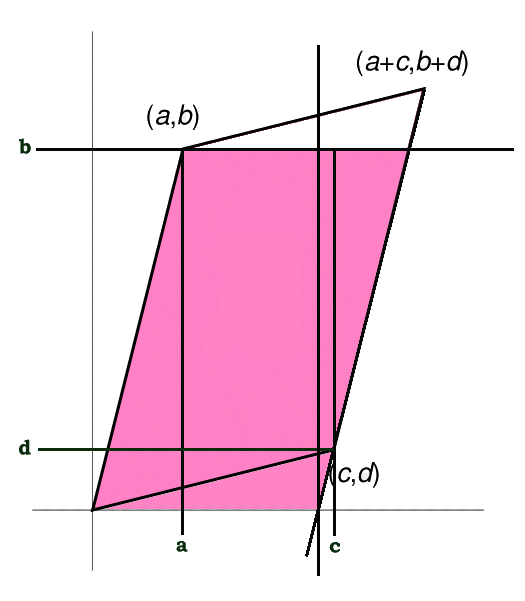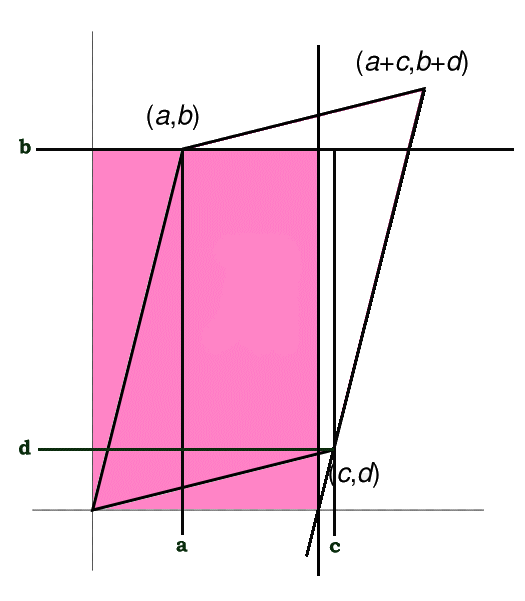
Numeric Example
[pmath] det (matrix{2}{2}{2 1 1 2}) = 2 * 2 – 1 * 1 = 3 [/pmath]
Compare that with the old fashioned area of two triangles that make up the parallelogram:
[pmath] Area Paralelogram = 2 * {1/2} * Base * Height [/pmath]
Using Pythagoras:
[pmath] Height = {3/sqrt{2}} [/pmath]
[pmath] Base = sqrt{2} [/pmath]
[pmath] Area Parallelogram = sqrt{2} * {3/sqrt{2}} = 3 [/pmath]
This carries on through higher dimensions. Below depicts a 3 variable system.
The rows r1, r2, r3 are vectors each. The various summations taken 1, 2 and 3 at a time define a parallelepiped.
The following excerpt is from X and may yield some insight when maximum entropy principle is applied. ( still working on this )
The moving rocks, also known as sliding rocks or sailing stones, are a geological phenomenon found in Racetrack Playa, a seasonally dry lake (a playa) located in the Panamint Mountains in Death Valley NationalPark, California. The rocks move across the surface of the playa, leaving long tracks behind them Read more…
Research Links
In many physical systems the question arises what is the probability distribution that describes a system with a given expected energy E over the interval from -infinity to + infinity? Again you will use the maximum entropy principle to determine this.
The constraints are as follows:
